SkipList原理及实现

重点

randLevel算法

/**
 * Redis实现
 * 初始层数为1，每次随机生成一个随机数，取低16位
 * 当取的这个值小于0.25倍的0xFFFF时，level++，否则退出。
 * 返回level和maxLevel的最小值
 *
 * 这里的ZSKIPLIST_P是晋升的概率。对应的期望层高是E=1/(1-p)。
 */
#define ZSKIPLIST_MAXLEVEL 64
#define ZSKIPLIST_P 0.25
private int randLevel() {
    int level = 1;
    while ((random() & 0xFFFF) < (ZSKIPLIST_P * 0xFFFF))
        level += 1;
    return (level < ZSKIPLIST_MAXLEVEL) ? level : ZSKIPLIST_MAXLEVEL;
}

跳表

论文地址

简介

SkipList是用于有序元素序列快速搜索查找的一个数据结构，跳表是一个随机化的数据结构，实质就是一种可以进行二分查找的有序链表。跳表在原有的有序链表上面增加了多级索引，通过索引来实现快速查找。跳表不仅能提高搜索性能，同时也可以提高插入和删除操作的性能。它在性能上和红黑树，AVL树不相上下，但是跳表的原理非常简单，实现也比红黑树简单很多。

下图是一个简单的skiplist

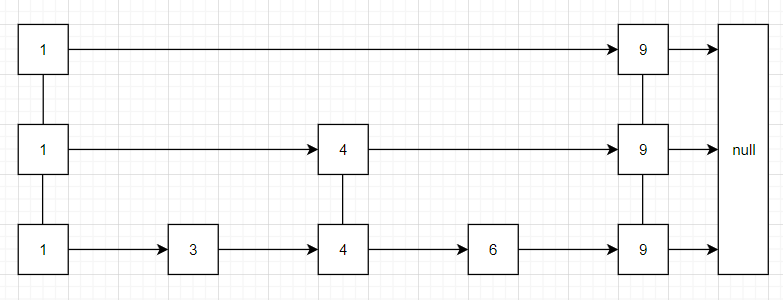
原理

说白了就是一个有序链表加上索引，以空间换时间。

结构

public class SkipList {
    private Node header;
    private Node tail;
    private long length;
    private int maxLevel;
    private int level;
    
    public Class Node {
        /** 用来保存该节点所记录的层数 */
        private List<Node> levels;
        /** 用来保存该节点的数据 */
        private Entry entry;
        /** 用来记录该节点的分数 */
        private float score;
    }
}

Get

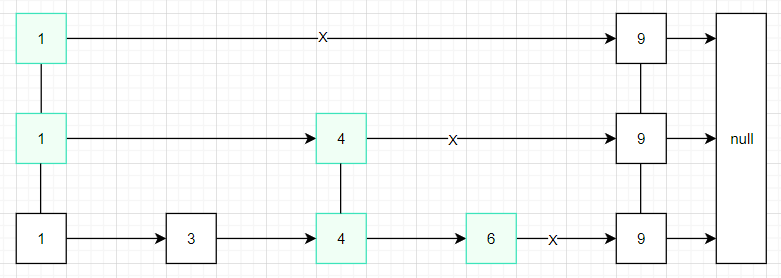
如果我们需要查询6这个位置的数据

skiplist会进行如下查询：

1. 先从节点1的最高层进行与下一个节点9进行比较，小于节点9，层数降低。
2. 再将节点1与下一个节点4进行比较，大于节点4，指针指向节点4。
3. 然后将节点4与节点9进行比较，小于节点9层数降低。
4. 将节点4与节点6比较，这时候找到了需要查询的节点，进行返回。

（如果层数的最低层并且没找到就返回null）

public byte[] get(byte[] key) {
    // 计算key的分数
    // calcScore()函数类似hash，功能是将key转换为一个对应的float值
    // 方便比较，这样就需要函数比较高效。
    float score = calcScore(key);
    List<Node> levels = header.levels;
    // 首先先遍历节点的levels
    for (int i = level - 1; i >= 0; i--) {
        Node next = levels.get(i);
        // 直到当前level的下一个节点的score小于当前的score
        while (next != null) {
            // 将当前的score和下一个的进行比较
            int flag = compare(score, key, next);
            if (flag == 0) {
                // 相同
                return next.getEntry().value;
            } else if (flag == -1){
                // 小于，下一层
                break;
            }
            // 大于
            // 从下一个节点开始找
            levels = next.levels;
            next = levels.get(i);
        }
    }
    return null;
}

Add

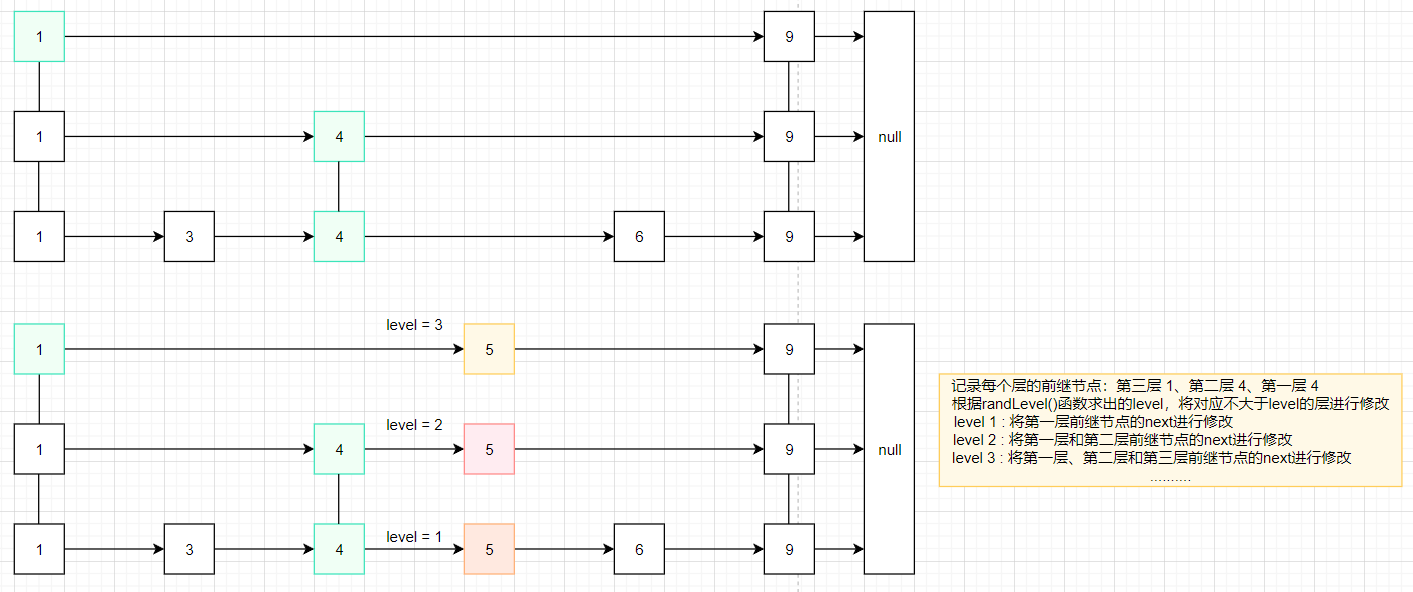
与查找的方法类似，但是需要记录查找所经过的节点。

如果我们需要添加节点5

public boolean add(Entry entry) {
    float score = calcScore(entry.key);
    // 前继节点
    Node[] preNode = new Node[level];
    // 找插入的位置
    Node p = header;
    // 竖着找
    // 遍历节点p的levels
    List<Node> levels = p.levels;
    Node next;
    for (int i = level - 1; i >= 0; i--) {
        // 获取该层的next节点
        next = levels.get(i);
        // 横向找，直到下一个分数大于等于当前分数或者下一个为null
        while (next != null) {
            // 与当前key进行比较
            int flag = compare(score, entry.key, next);
            if (flag == -1) {
                // 下一层
                break;
            } else if (flag == 0) {
                // 相同，直接修改并返回
                size += entry.size() - next.entry.size();
                next.entry = entry;
                return true;
            }
            // 下一个节点
            p = next;
            levels = p.levels;
            next = levels.get(i);
        }

        // 添加前继节点
        preNode[i] = p;
    }
    // 构建新节点
    Node newNode = new Node(entry, score);
    // 获取新节点层数
    int cLevel = randLevel();
    int minLevel = Math.min(cLevel, level);
    // 添加节点
    for (int i = 0; i < minLevel; i++) {
        Node swap = preNode[i].levels.get(i);
        preNode[i].levels.set(i, newNode);
        newNode.addLevel(swap);
    }
    // 判断是否需要增加层数
    while (cLevel > level) {
        // 将头节点层数增加
        header.levels.add(newNode);
        newNode.addLevel(null);
        level++;
    }
    length++;
    size += entry.size();
    return true;
}